"Chapter. 0 - 함수의 연속"
게시글 주소: https://iu.orbi.kr/00071303686
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

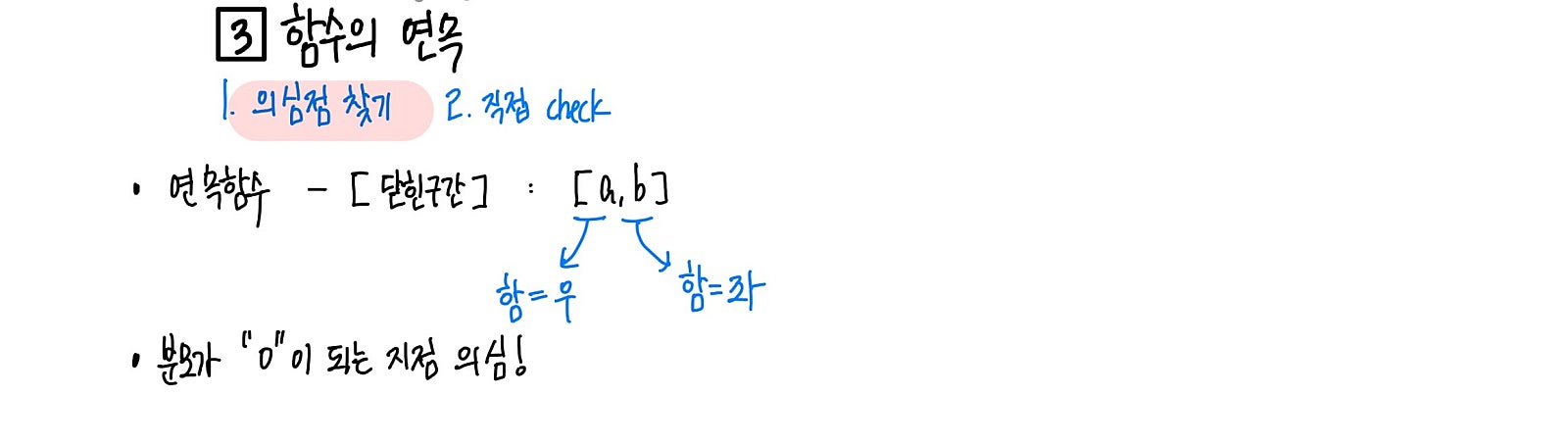
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
가천약 합격 5
와~~ 달달하네요
-
나도 거르고 싶긴 한데 대학 단톡방 공지방이 죄다 카톡이잖아 이걸 거르면 대학생활은...
-
34145 아예 처음부터 재수할작정으로 진학사도 안샀는데
-
삼수 의미있냐
-
계신가요?
-
보통 어디 선택하시나요?
-
어차피 섭종할 거 과세표준 싹 다 무시하고 모든 세금 세율 99% 만들자
-
자유'민주당'도 민주당이긴 함뇨
-
올해 사수해서 의대 붙은 애가 걍 지금 군대 가는게 맞냐는데
-
아아 이슬같이 죽겠노라
-
소득세 60% 빔..!
-
오르비에서 분탕쳐도 안잡혀감? 좋은데? 국회의원간다
-
7모 수학 성적 8
07인데 25수능 76?점 받고 3등급 떴던거같은데 엊그제 24 7모 88점 뜨고...
-
윤석열 안타깝다 11
민주당 찢새끼 씹준석 보기 좆같은데
-
지금까지 뭐했어 2
뭐했
-
문재인 좆됐다 이젠 진짜 끝났다 수사 들어간다 소식만 들리고 끝의 끝까지 뭉갠게...
-
제가 장난에 과민반응한 거면 죄송하고 좀 쉬고 오겠음요.
-
검찰, ‘문재인 정부 사드 정보 유출 의혹’ 압수수색 23
검찰이 문재인 정부가 사드(THAAD·고고도 미사일 방어체계) 배치를 늦추기 위해...
-
이재명은 극우 쓰레기임 ㅇㅇ
-
민주파출소에서 0
할수 있는게 뭐임? 내란선동죄로 고발도 안된다고하는데 허위사실유포,명예훼손이런거로 고발하려나
-
형님빽만
-
상당히 진지합니다
-
我支持民主党执政。 19
-
민주당 그 새끼들은 이미 명예훼손, 모욕죄를 법리까지 비틀며 성범죄에 편입시켜서 저...
-
가문의 영광 6
어릴때 분당 중앙공원에서…
-
대재명
-
다들 나니는 대학교에 공식적인 학과별 축구리그 있음? 3
전적대엔 있었는데 바뀌는 학교에 있을까싶네 없으면 안되는데 최대도파민인데 대학생활
-
韩国人民和全体奥尔比人民支持习近平主席和李在明总统。...
-
미적 확통 중에 1
수학 높2~낮1을 바라면 어떤게 낫나요? 작수 미적했는데 68점 나와서 ......
-
미성T개이쁘네 4
남친부렂다
-
오늘 운동 못하겠네..
-
명문대 자리 좀 만듭시다
-
물론 나같은 일개 소시민의 삶에 아무도 관심없겠지만 그래도 난 검열과 감시가 싫음...
-
대북송금을 하며 3
종북 간첩이 아니라는건 뭐죠
-
계세요? 즉 그때 탄핵이 가결되는게 맞았다 라고 생각하는 분이요
-
국지전 의견까지 나왔는대 이걸 쉴드치노 ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ
-
수의대 재입학 시켜주세요ㅠ 일단 시대 재종 등록해야하나
-
신택스 알고리즘 리앤로 하고 9월까지 실모,주간지빼고 없던데데이정도면 꽤 컴팩트한편이죠?
-
잘하고있었구나
-
잘돌아가던 민주주의 시스템을 파괴하려한 내란수괴라서 애초에 전두환 노태우와 동격에...
-
뭐마시지
-
하.. 재수생인데 개념부터 다시 채우려고요
-
나는 2
강민철한테 디엠답장을받은사람이다 무려 열공하라고 했다고 하하하하하하하
-
동의할 사람이 그리 없을 것 같긴한데
-
뀨뀨 8
뀨우
-
팀 유승민 레츠고
-
라고 말하면 안되겠죠
-
Ez한 문제입니다 몇번급인지 모르겠어서 댓 좀











































