2021학년도 수능 가형 20번 어려운 이유 & 해설
게시글 주소: https://iu.orbi.kr/00033501365
2021학년도 수능 가형 20번 (by.csm).pdf
안녕하세요 CSM입니다.
20번 해설을 들고왔습니다.
현재 21번보다
체감 난이도가 높다고 여겨지는 20번입니다.
21번
체감난이도가 높은 이유는
1) 함수 g(x)의 치역설정
2) 정적분의 "결과값"을 통해 함수 개형추론
에 있어서 기존 기출에서
단단하게 연습하기 어려운 형태여서
학생들이 조금 풀기 어려워한 듯 보입니다.
먼저 교양적으로 알아야 할 사실은
아래 그림과 같이 삼각함수 반주기의
넓이(정적분값)를 빠르게 파악해야 합니다.
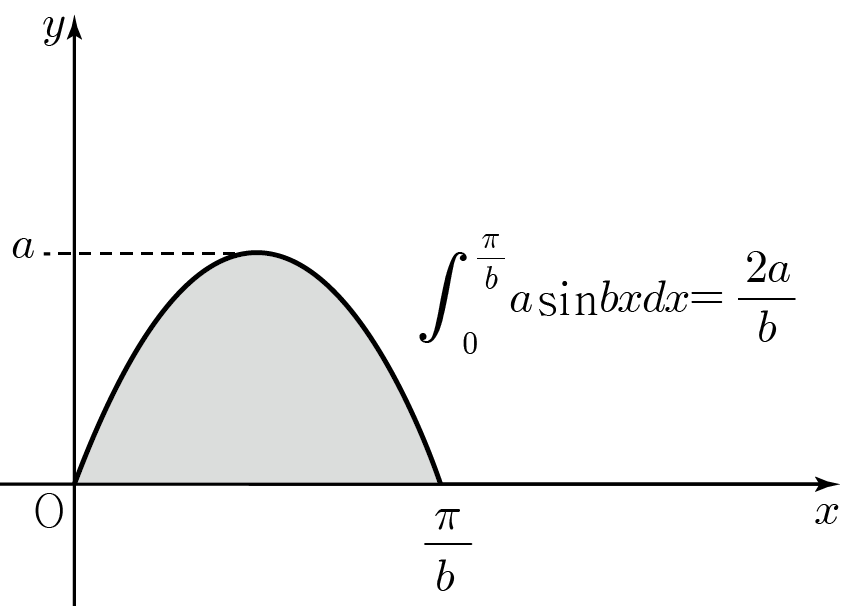
이를 토대로 해설은 다음과 같습니다. (아래 이미지 PDF도 첨부)
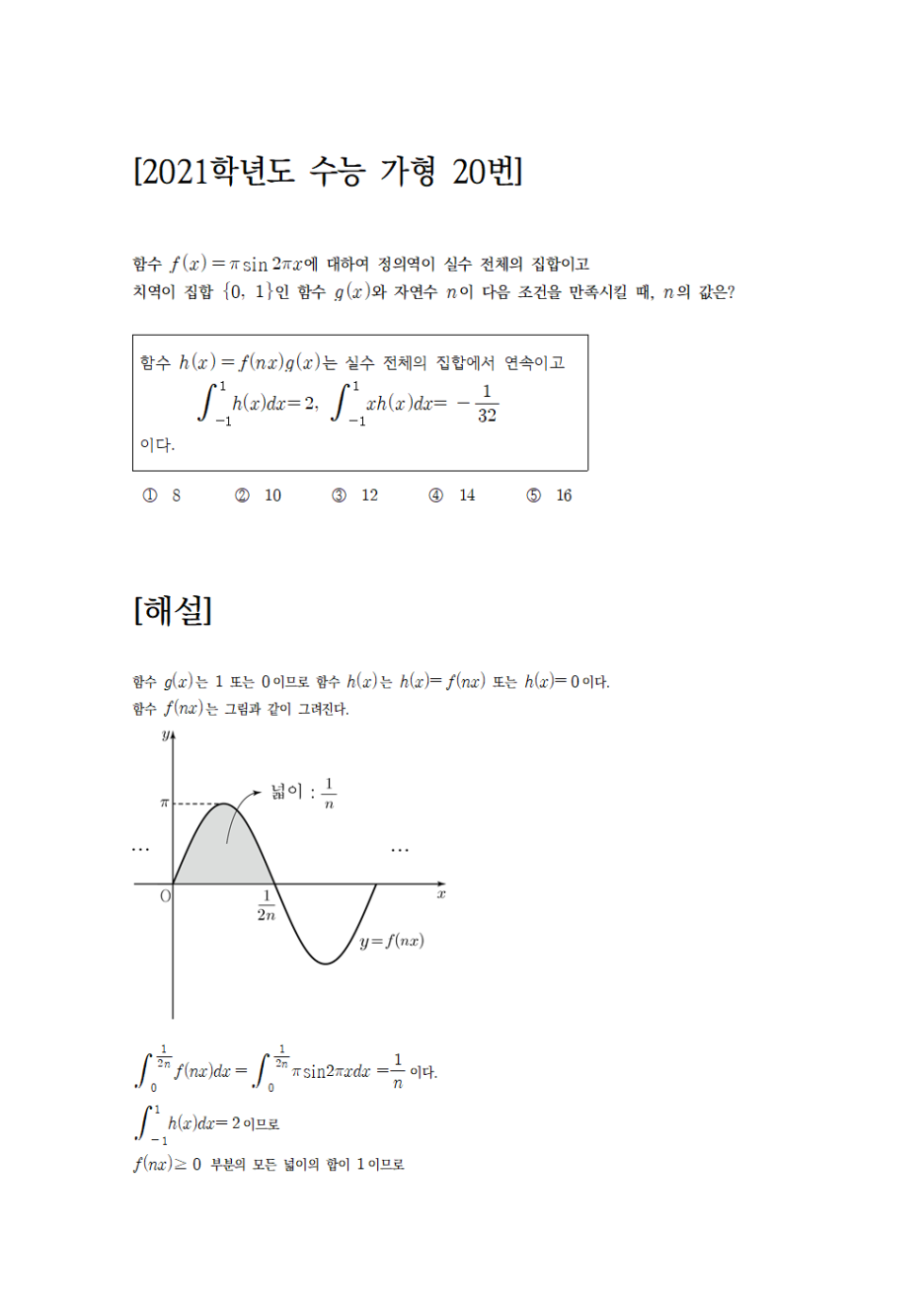
사진 설명을 입력하세요.
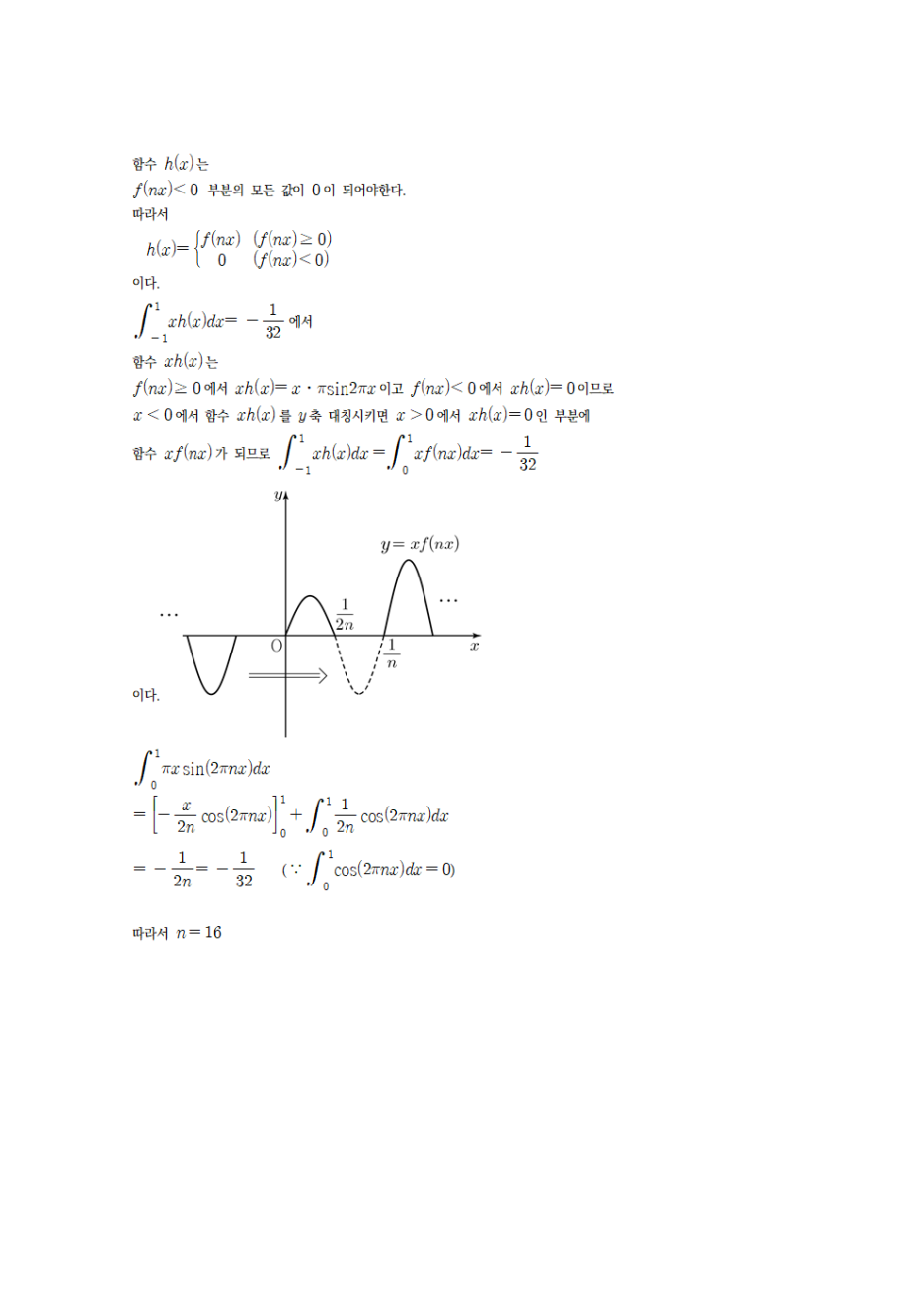
사진 설명을 입력하세요.
두가지 적분의 해석을 넓이관점과 식의 관점으로 보는 방향에 따라
풀이속도가 달라질 수 있는 문제이고 이런 경우에는
학생들에게 체감난이도 격차를 줄 수 있었던 문제라고 생각합니다.
도움이 되셨기를 바랍니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
이주호 사퇴해라 0
장관 2년 넘게 했으면 그만 해라
-
백분위 몇나올것같나요? 언매미적화지 97 100 1 50 47 입시끝ㄴㅐ게해주세오 ㅠ
-
(공/선) 미적 100 -> 100 142 미적 96 -> 99 139 미적 92...
-
결혼마렵다 5
네
-
우리 학교 특) 10
수학 내신 5등급 떠도 모고 2등급 나옴;; 본인 얘기임;;; ㅈ반 다니는 애들 볼 때마다 부러웠음
-
똥이 우선이지?
-
아이폰 16살까 1
se4나오면 그거 살까 흠
-
톰보이 개많이 들었는데.. 뭔가신기함
-
수학 황 질문 6
f프라임x의 거리가 2일때가 가, 나 조건을 만족한다고 했는데 만약 a를...
-
개씹노잼
-
내고향 서울엔 0
지금은 눈이 안와
-
놀라운 사실인데 일반고 기준으로 정시가 저점이 ㅈㄴ높음 대전 일반고 기준으로...
-
공대 기준으로 알려주세요 +인문계는 다 지원가능한가요?
-
알바면접가는데 3
늦게일어난 나
-
이거 긍정적인 효과인가요
-
오랜 데이터에서 나온 생각 물론 표본은 저 한명임
-
바로 내 팔로워를 뛰어 넘네
-
기차한번,지하철 두번타서 편도로 3시간 넘게 걸리는데 졸업식가려고 왕복 6시간을 버텨야되나…
-
채점결과 D-2 6
-
할거없는데 2
재수나할까
-
남녀공학 전환을 두고 학생들과 갈등을 겪고 있는 동덕여대가 학생들을 고소했다. 학교...
-
얼마나 빡세나여 광클한다고 하면
-
이기상 14
과 이 맘으로~~ 얼버기 히히
-
지듣노 2
LOVE SONG 가수 : 마히룽 성우 타카기 양에서도 소개된 노래입니다. 정말로...
-
내년에는 사탐 표본이 작년 원과목보다 더 고여있을 것 같은데 4
원과목 표점 떡상하고
-
자살이 아니라 살자가 됐으면..
-
중등기하 풀어라 2
-
설첨융가서 2
컴공처럼 전향가능해요? 이러면 얘기가 또 달라지는데
-
통장에 3
181원있음 머지
-
ㅇㅇ 사실 굉장히 잘 만남 살아보면서 느낀건데 능력있는 남자 = 예쁜 여자와...
-
성적 이정도인데 설컴은 안될거 같고 서울대 첨융이랑 연대 컴공이랑 붙으면 어디...
-
공부나 하라는 신의계시인가보다
-
코스트코나 트레이더스 가까움?
-
못지우는애들이 많을까 밖에선 일코하세요
-
[뉴테크] 척수손상 환자 다시 걸었다…뇌 심부자극으로 재활속도 높여 1
스위스 연구진, 보행에 영향 주는 뇌영역 찾아 환자의 뇌 깊은 곳에 전기자극,...
-
마음가짐 공부법 등등 삼수 꿀팁? 있나요
-
1컷이 45인게 주된 의견인거 같아서 ㅠㅠ 1컷이 45일때 44점 백분위는...
-
전문직은 일생을 살아가면서 남들이 자신을 보는 평가, 사회적 시선이 자신의 능력을...
-
좋아요정 뭐임 1
누가 계속 좋아요 눌러주는데
-
아가 기상 8
안뇽
-
2N년 동안 뚜벅이로 살던 냐가 하늘 퍼런 아침부터 운전면허학원에서 기능교육을 받고...
-
동덕여대 이슈 4
때문에 이대랑 숙대 선호도도 타격 있을까요?
-
과탐 가산점 4
과탐 가산점 3%, 5% 가 어느 정도인지 체감이 잘 안 가는데 얼마나 영향을 미치나요?
-
과탐 유지 0
내년 수능 연고 서성한 계약학과 목표로 하고있는데 과탐을 계속 해야할까요?
-
9모 55552 10모 풀 5등급입니다 국어 강기본(2월까지) 강기분 실모 수학...














































개인적으로 매우 친숙한 유형은 아니라고 생각합니다. 현장기준 어려웠을 것 같아요
asinbx 한칸넓이 a/b라서 n이 2의거듭제곱만 될거같아서 1.5중에 고민하고 5번 왼쪽정적분으로 계산해보니 사인 양수는 0곱해서 없어질것같고 음수는 -1곱해져서 양수가 될것같은 느낌으로 킹리적갓심씀
ㄹㅇ 걍 찍맞이네
아니에요 킹리적갓심은 절대 그냥 나오지 않습니다. 잘하셨습니다 ^__^
해설 잘 봤어요. 마지막에 정적분 int_{-1}^{1} xh(x)dx=int_{0}^{1} xf(nx)로 넘어가는 부분이 잘 이해가 안되는데 혹시 여유있으시다면 설명해주실 수 있을까요? 저는 사진처럼 풀었는데, 계산이 무척 더럽고 현장에서 저렇게 풀면 계산실수가 반드시 있을 것 같아서 부탁드립니다....(첫 줄의 오류는 건너뛰어주세요 고치기 귀찮아서...ㅎㅎ)
in_{-1}^{0}xh(x)dx 부분만 관찰해주시면 될 것 같습니다. 함숫값이 음수인 부분은 제거 되었을것이고 양수인부분만 남은 h(x)에 대하여 x를 곱하는데 x<0이므로 xh(x)<0가 됩니다.
따라서 xh(x)를 (-1,1)에서 그린 후 각각 적분을 하여도 괜찮습니다만,
(-1,0)인 부분을 그대로 y축 대칭시켜보면 결국 xf(nx)가 완성된다는 것을 알 수 있습니다.
이는 f(nx)가 처음부터 대칭함수이고 x를 곱하여서 '대칭성질'이 남아있다고 생각하여 판단할 수 있으며 이를 (-1, 0) => (0, 1)로 이동하는 치환적분하여 식적으로도 설명가능하나 이를 계산으로 의도하기보다는 최근 "영역관찰"을 포인트 잡아왔기에 그림도 적절히 섞어서 확인해주시면 될 것 같습니다.^^
아아아아 다 그대로 대칭되니까 그렇겠네요 감사합니다.
찍는게 더 빠를 듯. 2랑 1/32 나오고 f(nx) 주기가 1/n 이니까 8, 16 처럼 2의 거듭제곱꼴로 나오는 수가 답일 것 같고 8은 너무 작아서 16했는데 아.. 계산이 엄청 빡센거였네요
진짜 시험장에서 제일 어려웠어요... 30 20 이 최고봉.
이제 21 29 은 킬러 아닌듯해여ㅜ
와.. 그냥 1/2n~1/n, 1/n~3/2n 계속 적분해가면서 귀납적으로 적분값을 찾아냈는데 y축대칭하면 한번의 적분으로 풀리네요 진짜 충격이네